La conception intuitive qu’ont les élèves de la multiplication est celle de l’addition répétée. Bien que nécessaire de prime abord, elle se révèle insuffisante dès lors que les problèmes abordés relèvent par exemple du champ des nombres décimaux (sous-entendu non entiers). L’objectif de l’application accessible ici et présentée ci-dessous est de dépasser cette conception par l’introduction d’images mentales du produit de deux nombres. Cet outil paramétrable et vidéo-projetable s’appuie sur le concept de nombre rectangle. La démarche n’est qu’indicative et la notion nécessiterait bien entendu d’être travaillée plus longuement avec les élèves ; il ne s’agit ici que de présenter l’outil et sa motivation.
« L’apprentissage des structures multiplicatives dont font partie la multiplication, la division et les fractions, tout en relevant d’un socle commun, se répercute sur les apprentissages ultérieurs comme les raisonnements proportionnels et algébriques. »
De la multiplication au fractions : réconcilier intuition et sens mathématique (synthèse du CSEN)
Le produit 4 × 6 se représente par un rectangle de largeur 4 et de longueur 6. On ne parle pas ici d’aire (même si cette grandeur est intrinsèquement liée au concept) mais d’une répartition en 4 bandes de 6 unités (représentée chacune par un carré).
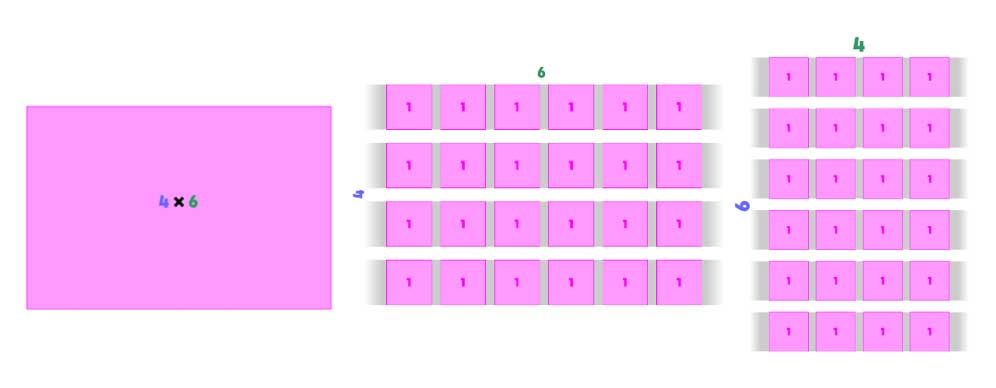
Cette représentation s’appuie sur la conception intuitive de la multiplication et permet de visualiser de façon évidente sa commutativité, en échangeant simplement la position des facteurs.
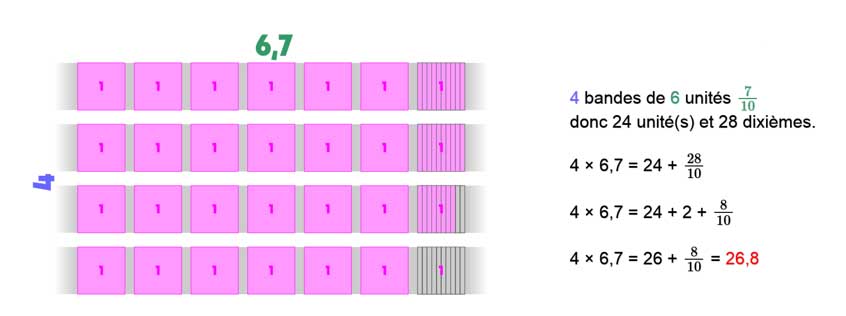
Cette conception intuitive peut encore être utilisée pour calculer le produit 4 × 6,7 : il s’agit là encore de le représenter par 4 bandes de 6 unités et 7/10. On dénombre alors 24 unités et 28 dixièmes qui permet à l’élève en s’appuyant sur sa connaissance de la fraction décimale d’aboutir au résultat escompté.
Le produit 6,7 × 4 est plus délicat à concevoir. On pourrait certes étendre la commutativité de la multiplication sur les entiers ou s’appuyer sur un argument géométrique pour affirmer qu’il est égal au produit 4 × 6,7 mais c’est à mon sens un raccourci à éviter :
- On ne pourra pas avoir la même démarche quand les deux facteurs seront décimaux.
- Dans une situation contextualisée, elle s’oppose trop frontalement à l’intuition : l’achat de 6,7 kg d’un produit à 4 € le kg est différent de l’achat de 4 kg d’un produit à 6,7 € le kg, même si au final, la somme payée est la même.
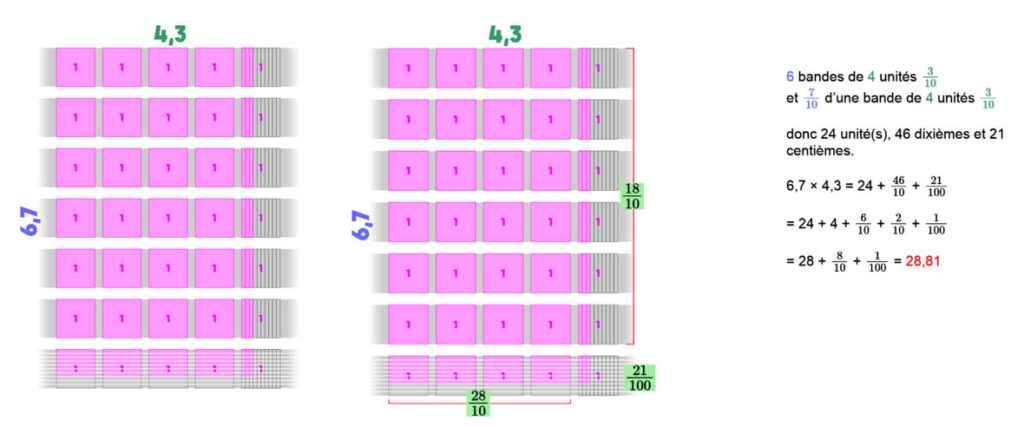
Aussi, on représentera dans un premier temps le produit 6,7 × 4 par 6 bandes de 4 unités et 7/10 d’une bande supplémentaire de 4 unités.
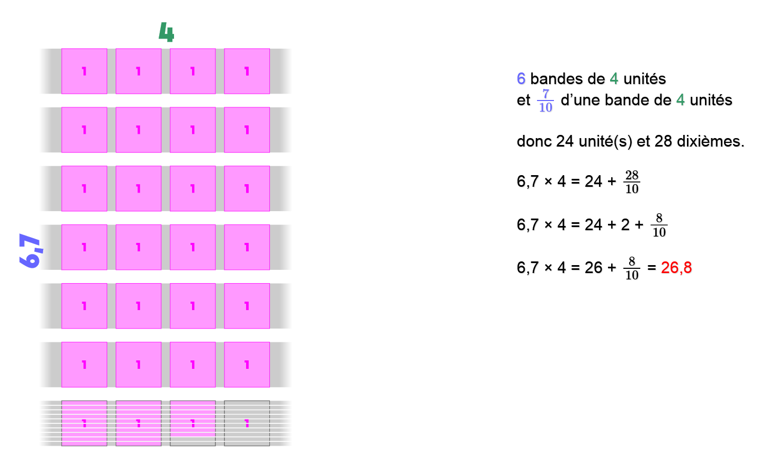
On ne manquera pas de faire remarquer que les résultats sont identiques et qu’il s’agit donc effectivement du même produit : la multiplication garde sa commutativité quand il s’agit de nombres décimaux.
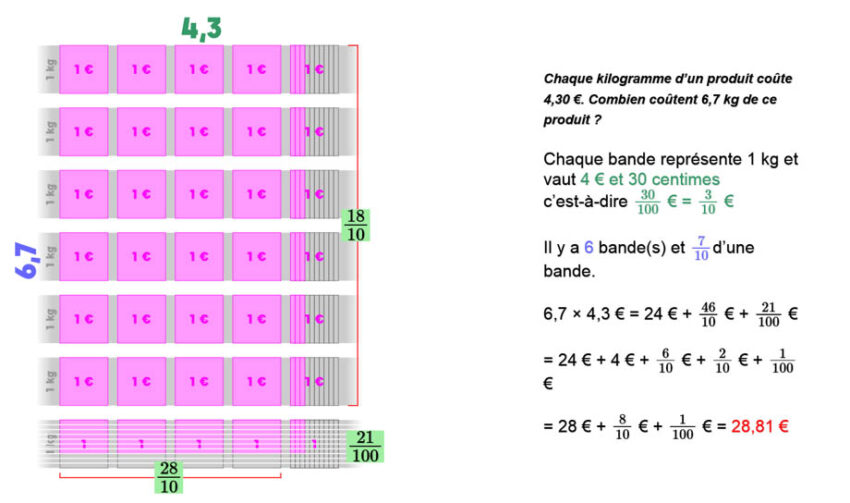
Le produit 6,7 × 4,3 constitue le dernier cas et se traite de façon identique. Le seul obstacle réside dans l’apparition des centièmes comme dixièmes de dixièmes, mais la difficulté est levée par la représentation.
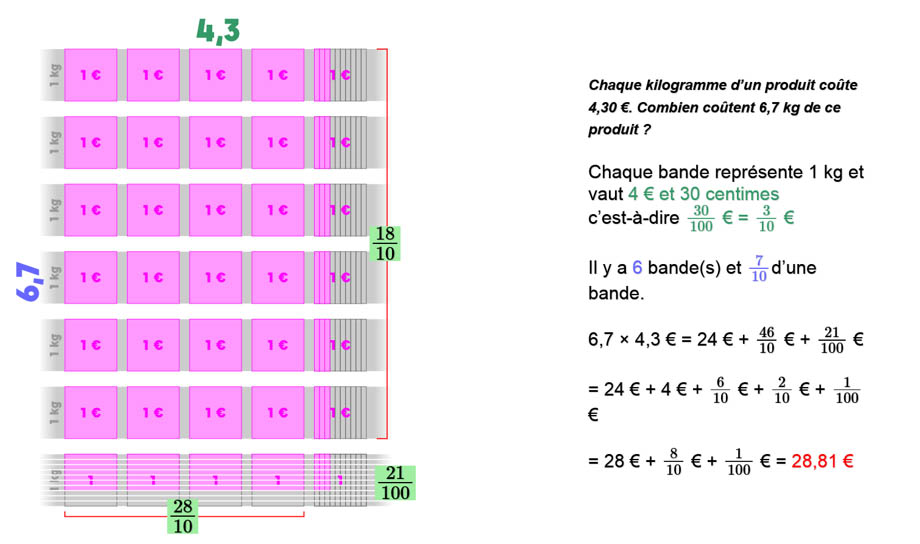
Cette représentation en rectangle permet d’aborder des situations contextualisées et de justifier le recours à la multiplication. Un exemple prototypique de prix au kilogramme peut se modéliser de façon analogue et exprime visuellement la similarité de la situation.
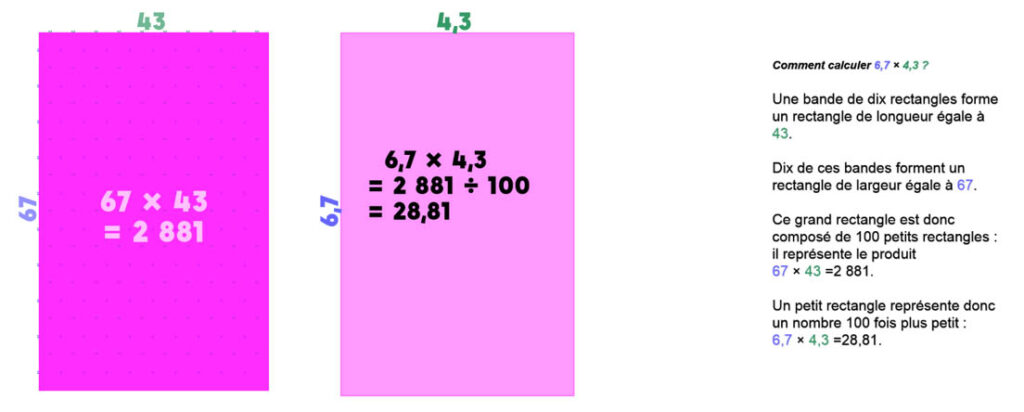
Évidemment, cette modélisation n’est que transitoire et on devra s’en détacher une fois l’automatisation acquise. Celle-ci passe d’abord par l’apprentissage d’un algorithme de calcul et là-encore, on peut s’appuyer sur le modèle du nombre rectangle.
Par exemple, en juxtaposant 100 rectangles représentant le produit 6,7 × 4,3 on fait apparaître le rectangle représentant 67 × 43 dont le calcul est connu des élèves.
Ces représentations figurées permettent de soutenir la compréhension des structures mathématiques multiplicatives et rendent visibles des propriétés pertinentes telles que la commutativité de la multiplication, la distributivité et la relation inverse entre multiplication et division… mais cela est une autre histoire.